Trigonometría
La trigonometría es una rama de la matemática, es el estudio de las razones trigonométricas: seno, coseno; tangente, cotangente; secante y cosecante. Interviene directa o indirectamente en las demás ramas de la matemática y se aplica en todos aquellos ámbitos donde se requieren medidas de precisión. La trigonometría se aplica a otras ramas de la geometría, como es el caso del estudio de las esferas en la geometría del espacio
Historia de la trigonometría
Los babilonios y los egipcios (hace más de 3000 años) fueron los primeros en utilizar los ángulos de un triángulo y las razones trigonométricas para efectuar medidas en agricultura y para construir pirámides. Posteriormente se desarrolló más con el estudio de la astronomía mediante la predicción de las rutas y posiciones de los cuerpos celestes y para mejorar la exactitud en la navegación y en el cálculo del tiempo y los calendarios.
El estudio de la trigonometría pasó después a Grecia, donde destaca el matemático y astrónomo Griego Hiparco de Nicea. Más tarde se difundió por India y Arabia donde era utilizada en la Astronomía. Desde Arabia se extendió por Europa, donde finalmente se separa de la Astronomía para convertirse en una rama independiente de las Matemáticas.
A finales del siglo VIII los astrónomos Árabes trabajaron con la función seno y a finales del siglo X ya habían completado la función seno y las otras cinco funciones. También descubrieron y demostraron teoremas fundamentales de la trigonometría.
A principios del siglo XVII, el matemático John Napier inventó los logaritmos y gracias a esto los cálculos trigonométricos recibieron un gran empuje.
A mediados del siglo XVII Newton encontró la serie para el sen x y series similares para el cos x y la tg x. Con la invención del cálculo las funciones trigonométricas fueron incorporadas al análisis, donde todavía hoy desempeñan un importante papel tanto en las matemáticas puras como en las aplicadas.
Razones trigonometricas

Gráficas del seno, el coseno y la tangente
Para abordad el tema de las gráficas primero necesitamos conocer algunos conceptos básicos.
PERIODO
El período de una función periódica es la parte de ésta que, conforme se le añade a la variable independiente, hace repetir los valores de la variable dependiente.
AMPLITUD
se denomina amplitud al rango de la función.
RANGO
Se denomina rango al intervalo entre el valor máximo y el valor mínimo.
PUNTOS MÁXIMOS Y MÍNIMOS
Los puntos máximos de una función son los que la amplitud de onda es el punto mas alto y los mínimos es el punto en que la amplitud es el punto mas bajo.
PUNTOS DE INTERSECCIÓN
Son los puntos en común que satisfacen las expresiones que forman parte de la intersección.
Gráfica del seno

Gráfica del coseno
Gráfica de la tangente

Identidades trigonometricas
son igualdades que involucran funciones trigonométricas. Estas identidades son siempre útiles para cuando necesitamos simplificar expresiones que tienen incluidas funciones trigonométricas, cualesquiera que sean los valores que se asignen a los ángulos para los cuales están definidas estas razones.Las identidades trigonométricas nos permiten plantear una misma expresión de diferentes formas. Para simplificar expresiones algebraicas, usamos la factorización, denominadores comunes, etc. Pero para simplificar expresiones trigonométricas utilizaremos estas técnicas en conjunto con las identidades trigonométricas.
Antes de comenzar a ver las diferentes identidades trigonométricas, debemos conocer algunos términos que usaremos bastante en trigonometría, que son las tres funciones más importantes dentro de esta. El coseno de un ángulo en un triángulo rectángulo se define como la razón entre el cateto adyacente y la hipotenusa:
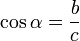
Otra función que utilizaremos en trigonometría es “seno”. Definiremos seno como la razón entre el cateto opuesto y la hipotenusa en un triángulo rectángulo:
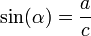
Mientras tanto la palabra tangente en matemática puede que tenga dos significados distintos. En geometría se utiliza el término de recta tangente, pero a nosotros en trigonometría nos interesa otro término que es el de tangente de un ángulo, el cual es la relación entre los catetos de un triángulo rectángulo , lo mimo que decir que es el valor numérico que resulta de dividir la longitud del cateto opuesto entre la del cateto adyacente al ángulo.
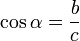
Otra función que utilizaremos en trigonometría es “seno”. Definiremos seno como la razón entre el cateto opuesto y la hipotenusa en un triángulo rectángulo:
Mientras tanto la palabra tangente en matemática puede que tenga dos significados distintos. En geometría se utiliza el término de recta tangente, pero a nosotros en trigonometría nos interesa otro término que es el de tangente de un ángulo, el cual es la relación entre los catetos de un triángulo rectángulo , lo mimo que decir que es el valor numérico que resulta de dividir la longitud del cateto opuesto entre la del cateto adyacente al ángulo.
Ejercicios de identidades trigonometricas
Comprobar las identidades trigonométricas:
1

2


3

4

Ley de los senos y cosenos
Ley de los senos
La ley de los senos establece que en cualquier triángulo la relación de cualquiera de sus lados al seno del ángulo opuesto es constante.
Comprobar las identidades trigonométricas:
1
2
3
4
Ley de los senos y cosenos
Ley de los senos
La ley de los senos establece que en cualquier triángulo la relación de cualquiera de sus lados al seno del ángulo opuesto es constante.
Escrita como fórmula, la ley de los senos es la siguiente:
a / sen A = b / sen B = c / sen C
Problema 1
Cuando el ángulo de elevación del sol es 64° un poste telefónico que esta inclinado un ángulo de 9° directamente frente al sol forma una sombra de 5,25 m de longitud en terreno horizontal. Calcule la longitud aproximada del poste.
Resolución:
En terreno plano se encuentra dos puntos P y Q en los lados opuestos de una montaña. Para calcular la distancia entre ellos, un topógrafo escoge un punto R a 50 m de P y a continuación determina que el ángulo PQR es de 37°. Calcule la distancia de P a Q.
Resolución:
Ley de los cosenos
Ley de los senos
La ley de los senos establece que en cualquier triángulo la relación de cualquiera de sus lados al seno del ángulo opuesto es constante.
Problema 1
Cuando el ángulo de elevación del sol es 64° un poste telefónico que esta inclinado un ángulo de 9° directamente frente al sol forma una sombra de 5,25 m de longitud en terreno horizontal. Calcule la longitud aproximada del poste.
Resolución:
Problema 2
En terreno plano se encuentra dos puntos P y Q en los lados opuestos de una montaña. Para calcular la distancia entre ellos, un topógrafo escoge un punto R a 50 m de P y a continuación determina que el ángulo PQR es de 37°. Calcule la distancia de P a Q.
Resolución:
Problemas aplicando la ley de los cosenos
Problema 1:
En el triángulo de la figura, hallar la longitud del lado rotulado con x
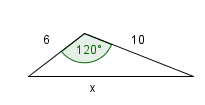
Solución:
Como conocemos dos lados adyacentes y el ángulo entre ellos, podemos aplicar la ley de cosenos, así:
Ley de los senos
La ley de los senos establece que en cualquier triángulo la relación de cualquiera de sus lados al seno del ángulo opuesto es constante.
Escrita como fórmula, la ley de los senos es la siguiente:
a / sen A = b / sen B = c / sen C
Problema 1
Cuando el ángulo de elevación del sol es 64° un poste telefónico que esta inclinado un ángulo de 9° directamente frente al sol forma una sombra de 5,25 m de longitud en terreno horizontal. Calcule la longitud aproximada del poste.
Resolución:
En terreno plano se encuentra dos puntos P y Q en los lados opuestos de una montaña. Para calcular la distancia entre ellos, un topógrafo escoge un punto R a 50 m de P y a continuación determina que el ángulo PQR es de 37°. Calcule la distancia de P a Q.
Resolución:
Ley de los cosenos
La ley de los cosenos establece que c2 = a2 + b2 - 2ab cos C.
Nos permite calcular el tercer lado desconocido cuando se conocen dos lados y el ángulo.
Igualmente,
a2 = b2 + c2 - 2bc cos A
y
b2 = c2 + a2 - 2ca cos B
y
b2 = c2 + a2 - 2ca cos B
Problemas aplicando la ley de los cosenos
Problema 1:
En el triángulo de la figura, hallar la longitud del lado rotulado con x

Solución:
Como conocemos dos lados adyacentes y el ángulo entre ellos, podemos aplicar la ley de cosenos, así:
 Problema 2: En el triángulo de la figura, hallar la longitud del lado rotulado con x  Solución: Como conocemos dos lados adyacentes y el ángulo entre ellos, podemos aplicar la ley de cosenos, así:
|


































No hay comentarios:
Publicar un comentario